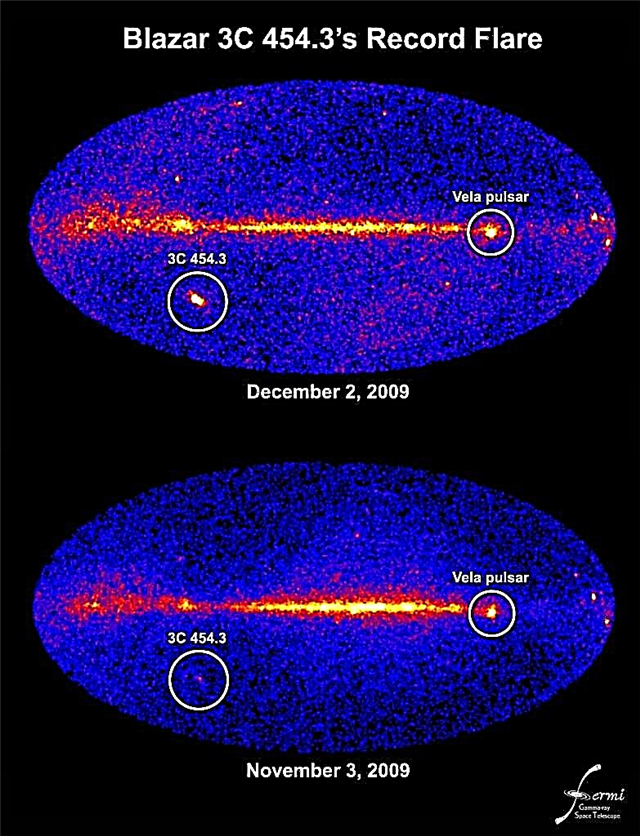
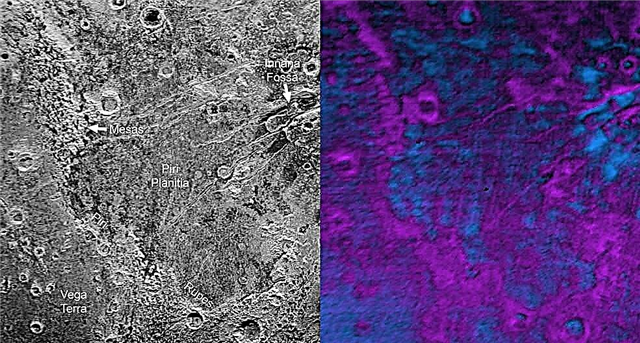
Légende: Vue de la lune au périgée et à l'apogée
En tant que professeur, je suis toujours à la recherche de laboratoires avec des configurations simples adaptées aux étudiants. Mon préféré actuel est de trouver la vitesse de la lumière avec du chocolat.
Dans un nouveau document récemment téléchargé sur arXiv, Kevin Krisciunas de Texas A&M décrit une méthode pour déterminer l'excentricité orbitale de la lune avec une erreur étonnamment faible en utilisant rien de plus qu'un mètre, un morceau de carton et un programme destiné à ajuster les courbes à étoiles variables.
Cette méthode utilise le fait que l'excentricité peut être déterminée à partir du rapport de la taille angulaire moyenne d'un objet et de la moitié de son amplitude. Ainsi, l'objectif principal est de mesurer ces deux quantités.
Pour ce faire, la stratégie de Kevin consiste à utiliser un trou de visée en carton qui peut glisser le long d'un mètre. En regardant à travers le trou à la lune et en faisant glisser la carte d'avant en arrière jusqu'à ce que la taille angulaire du trou chevauche juste la lune. De là, le diamètre du trou divisé par la distance en bas du mètre donne la taille angulaire grâce à la formule du petit angle (? = D / D en radians si D >> d).
Pour éviter les erreurs systématiques de mauvaise évaluation lorsque la carte est glissée vers l'avant jusqu'à ce que la taille du trou corresponde à la lune, il est préférable de l'approcher également de l'autre sens; En venant de l'extrémité du mètre. Cela devrait aider à réduire les erreurs et lors de la tentative de Kevin, il a constaté qu'il avait un écart type de ± 4 mm lors de cette opération.
À ce stade, il y a encore une autre erreur systématique à prendre en compte: la pupille a une taille finie comparable au trou de visée. Cela entraînera une sous-estimation de la taille angulaire réelle. En tant que tel, un facteur de correction est nécessaire.
Pour dériver ce facteur de correction, Kevin a placé un disque de 91 mm à une distance de 10 mètres (cela devrait produire un disque avec la même taille angulaire que la lune vu de cette distance). Pour produire le meilleur match, le glissement de carton avec le trou de visée devrait doivent être placés à 681,3 mm sur le mètre, mais en raison de l'erreur systématique de la pupille, Kevin a constaté qu'il devait être placé à 821 mm. Le rapport du placement observé au placement correct a fourni le facteur de correction utilisé par Kevin (1,205). Cela devrait être calibré pour chaque personne et dépendrait également de la quantité de lumière pendant le temps d'observation car cela affecte également le diamètre de la pupille. Cependant, l'adoption d'un seul facteur de correction donne des résultats satisfaisants.
Cela permet d'obtenir des données correctement prises qui peuvent ensuite être utilisées pour déterminer les quantités nécessaires (la taille angulaire moyenne et la moitié de l'amplitude). Pour les déterminer, Kevin a utilisé un programme connu sous le nom de PERDET qui est conçu pour ajuster les courbes sinusoïdales aux oscillations des étoiles variables. Tout programme qui pourrait adapter de telles courbes aux points de données en utilisant un?2 fit ou une analyse de Fourier conviendrait à cette fin.
A partir de tels programmes, une fois que la taille angulaire moyenne et la demi-amplitude sont déterminées, leur rapport fournit l'excentricité. Pour l'expérience de Kevin, il a trouvé une valeur de 0,039 ± 0,006. De plus, la période qu'il a déterminée de périgée en périgée était de 27,24 ± 0,29 jours, ce qui est en excellent accord avec la valeur acceptée de 27,55 jours.