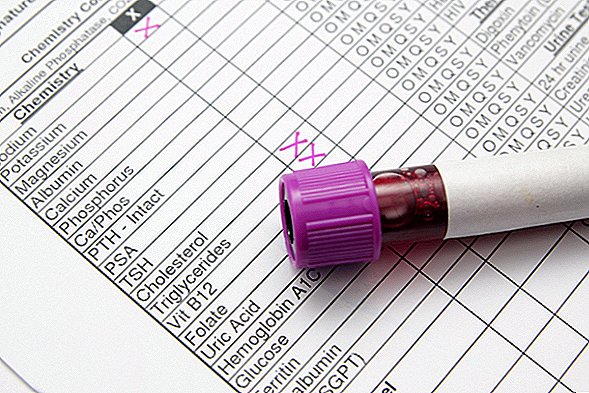
La théorie du chaos est démontrée dans cette image, qui a été créée avec une longue exposition d'une lumière au bout d'un double pendule.
(Image: © Wikimedia Commons / Cristian V.)
Ce serait vraiment bien de connaître les prévisions météorologiques non seulement une semaine à l'avance, mais un mois, voire une année dans le futur. Mais la prévision du temps présente un certain nombre de problèmes délicats que nous ne pourrons jamais résoudre entièrement. La raison n'est pas seulement la complexité - les scientifiques abordent régulièrement des problèmes complexes avec facilité - c'est quelque chose de beaucoup plus fondamental. C'est quelque chose découvert au milieu du 20e siècle: la vérité que nous vivons dans un univers chaotique qui, à bien des égards, est complètement imprévisible. Mais cachés au fond de ce chaos se trouvent des schémas surprenants, schémas qui, si nous sommes jamais capables de les comprendre pleinement, pourraient conduire à des révélations plus profondes.
Comprendre le chaos
L'une des belles choses de la physique est qu'elle est déterministe. Si vous connaissez toutes les propriétés d'un système (où "système" peut signifier quelque chose d'une seule particule dans une boîte aux modèles météorologiques sur la Terre ou même l'évolution de l'univers lui-même) et vous connaissez les lois de la physique, alors vous pouvez prédire parfaitement l'avenir. Vous savez comment le système évoluera d'un État à l'autre au fil du temps. C'est du déterminisme. C'est ce qui permet aux physiciens de faire des prédictions sur la façon dont les particules et la météo et l'univers entier évolueront avec le temps.
Il s'avère cependant que la nature peut être à la fois déterministe et imprévisible. Nous avons d'abord eu des indices de cette façon dans les années 1800, lorsque le roi de Suède a offert un prix à quiconque pouvait résoudre le soi-disant problème des trois corps. Ce problème concerne la prédiction du mouvement selon les lois d'Isaac Newton. Si deux objets du système solaire n'interagissent que par gravité, les lois de Newton vous indiquent exactement comment ces deux objets se comporteront bien dans le futur. Mais si vous ajoutez un troisième corps et que vous le laissez jouer le jeu gravitationnel aussi, alors il n'y a pas de solution et vous ne pourrez pas prédire l'avenir de ce système.
Le mathématicien français Henri Poincaré (sans doute un supergenius) a remporté le prix sans vraiment résoudre le problème. Au lieu de le résoudre, il a écrit sur le problème, décrivant toutes les raisons pour lesquelles il n'a pas pu être résolu. L'une des raisons les plus importantes qu'il a soulignées était la façon dont de petites différences au début du système entraîneraient de grandes différences à la fin.
Cette idée a été largement abandonnée, et les physiciens ont continué, en supposant que l'univers était déterministe. C'est-à-dire qu'ils l'ont fait jusqu'au milieu du 20e siècle, lorsque le mathématicien Edward Lorenz étudiait un modèle simple de la météo terrestre sur un ordinateur ancien. Quand il a arrêté et relancé sa simulation, il s'est retrouvé avec des résultats extrêmement différents, ce qui ne devrait pas être une chose. Il introduisait exactement les mêmes entrées, et il résolvait le problème sur un ordinateur, et les ordinateurs sont vraiment bons pour faire exactement la même chose encore et encore.
Il a découvert une sensibilité surprenante aux conditions initiales. Une petite erreur d'arrondi, pas plus d'une partie sur un million, entraînerait un comportement complètement différent des conditions météorologiques dans son modèle.
Ce que Lorenz a découvert essentiellement, c'est le chaos.
Trébuchant dans le noir
C'est le signe signature d'un système chaotique, tel qu'identifié pour la première fois par Poincaré. Normalement, lorsque vous démarrez un système avec de très petits changements dans les conditions initiales, vous n'obtenez que de très petits changements dans la sortie. Mais ce n'est pas le cas avec la météo. Un tout petit changement (par exemple, un papillon battant des ailes en Amérique du Sud) peut entraîner une énorme différence de temps (comme la formation d'un nouvel ouragan dans l'Atlantique).
Les systèmes chaotiques sont partout et, en fait, dominent l'univers. Collez un pendule à l'extrémité d'un autre pendule, et vous avez un système très simple mais très chaotique. Le problème des trois corps intrigué par Poincaré est un système chaotique. La population des espèces au fil du temps est un système chaotique. Le chaos est partout.
Cette sensibilité aux conditions initiales signifie qu'avec des systèmes chaotiques, il est impossible de faire des prédictions fermes, car on ne peut jamais connaître exactement, précisément, à la virgule décimale infinie, l'état du système. Et si vous êtes encore plus petit, après assez de temps, vous n'aurez aucune idée de ce que fait le système.
C'est pourquoi il est impossible de prédire parfaitement la météo.
Les secrets des fractales
Il y a un certain nombre de caractéristiques surprenantes enfouies dans cette imprévisibilité et ce chaos. Ils apparaissent principalement dans quelque chose appelé espace des phases, une carte qui décrit l'état d'un système à différents moments. Si vous connaissez les propriétés d'un système à un «instantané» spécifique, vous pouvez décrire un point dans l'espace des phases.
Au fur et à mesure qu'un système évolue et change son état et ses propriétés, vous pouvez prendre un autre instantané et décrire un nouveau point dans l'espace des phases, en créant au fil du temps une collection de points. Avec suffisamment de tels points, vous pouvez voir comment le système s'est comporté au fil du temps.
Certains systèmes présentent un motif appelé attracteurs. Cela signifie que peu importe où vous démarrez le système, il finit par évoluer vers un état particulier qu'il affectionne particulièrement. Par exemple, peu importe où vous déposez une balle dans une vallée, elle se retrouvera au fond de la vallée. Ce fond est l'attracteur de ce système.
Lorsque Lorenz a regardé l'espace de phase de son modèle météorologique simple, il a trouvé un attracteur. Mais cet attracteur ne ressemblait à rien de ce qui avait été vu auparavant. Son système météorologique avait des modèles réguliers, mais le même état n'a jamais été répété deux fois. Il n'y a jamais deux points dans l'espace des phases qui se chevauchent. Déjà.
Contradiction
Il y a un certain nombre de caractéristiques surprenantes enfouies dans cette imprévisibilité et ce chaos. Déjà.
Cela semblait être une contradiction évidente. Il y avait un attracteur; c'est-à-dire que le système avait un ensemble d'états préféré. Mais le même état n'a jamais été répété. La seule façon de décrire cette structure est comme une fractale.
Si vous regardez l'espace de phase du système météorologique simple de Lorenz et zoomez sur un petit morceau de celui-ci, vous verrez une version minuscule du même espace de phase. Et si vous prenez une plus petite partie de cela et que vous zoomez à nouveau, vous verrez une version plus petite du même attracteur. Et ainsi de suite et ainsi de suite à l'infini. Les choses qui se ressemblent plus vous les regardez de près sont des fractales.
Le système météorologique a donc un attracteur, mais c'est étrange. C'est pourquoi ils sont littéralement appelés attracteurs étranges. Et ils surgissent non seulement par temps, mais dans toutes sortes de systèmes chaotiques.
Nous ne comprenons pas pleinement la nature des attracteurs étranges, leur signification ou comment les utiliser pour travailler avec des systèmes chaotiques et imprévisibles. Il s'agit d'un domaine relativement nouveau des mathématiques et des sciences, et nous essayons toujours d'envelopper nos têtes autour de lui. Il est possible que ces systèmes chaotiques soient, dans un certain sens, déterministes et prévisibles. Mais cela reste à déterminer, donc pour l'instant, nous n'aurons qu'à nous contenter de nos prévisions météo pour le week-end.
- Comment annuler temporairement le chaos sans fin de l'univers avec le chloroforme
- Les signes du chaos | Fond d'écran Espace
- Chaos chaud | Fond d'écran Espace
Paul M. Sutter est astrophysicien à Université d'État de l'Ohio, hôte de "Demandez à un astronaute" et "Radio spatiale, "et auteur de"Votre place dans l'univers."
En savoir plus en écoutant l'épisode "L'univers est-il vraiment prévisible?" sur le podcast "Ask a Spaceman", disponible sur iTunes et sur le Web à http://www.askaspaceman.com.
Merci à Carlos T., Akanksha B., @TSFoundtainworks et Joyce S. pour les questions qui ont mené à cette pièce! Posez votre propre question sur Twitter en utilisant #AskASpaceman ou en suivant Paul @PaulMattSutter et facebook.com/PaulMattSutter.